— Tips:点击上方【憨爸在美国】查看往期内容 —
前段时间有个朋友发给我一道数学应用题,问我该怎么教孩子解?

看到题目后,我就随手在纸上画了一张图,啥也没解释就发给了她。

结果朋友一看到我的图,尽管没有文字说明,她也瞬间明白了!

这就是数学思维里“建模”的力量,对孩子和家长都非常管用!如果孩子学会建模,那么在做数学里最难的应用题时,都会做得非常轻松!而如果家长学会建模,那么给孩子解释数学问题也会很容易,一张图就能让对方秒懂!
Part.1 什么是建模?
建模是新加坡数学里最基础的教学方法,这个方法在亚洲数学教学里非常普及,后来流传到美国,在课堂里也得到大量的使用。
我以前介绍过建模,其实它就是把文字转化为数学图形的一种方法。
比如说我们要求解:3 + 4 = ?
那么我们可以画一张下面这样的方格图,小一点的方格代表3,大一点的方格代表4,这样合起来就是“3+4”了!

或许你觉得这个有点多此一举,“3+4”还不简单,直接算成7就好,何必画图建模呢?但是我如果举一个复杂点的例子,你就知道这么做的好处了!
我把题目改一改,说:
“爸爸在桌上放了3个桔子,妈妈又在桌上放了4个桔子,一共有多少个?”
如果孩子不晓得如何列出数学表达式的话,那么他们就可以先建模,画出下面这幅图,接着通过图就知道应该列出数学表达式“3+4”了!

如果我把题目再改一改,说:
“爸爸有3个桔子,妈妈比爸爸多4个桔子,妈妈一共有多少个桔子?”
你看同样是爸爸妈妈的桔子问题,但后一种题目的表达方式和前一种完全不同,前者是求解“总和问题”,后者是求解“比较问题”。虽然类型不一样,但是我们依然可以画出同样的下面这张建模图,从而得到同样的数学表达式“3+4”!

这就是建模的魅力,不管多复杂的问题,不管这个题目怎么变化,只要孩子读懂题目,建出模型,就能将题目解答出来。
Part.2 怎样建模?
建模的核心是阅读理解,而且要求孩子掌握文章的关键词,逐步将建模的图给画出来!
这里举一个例子:
Maria’s going to celebrate her birthday at home and invited 20 classmates. If we know that 3/5 of the class are girls and the rest are boys, how many girls did Maria invite to her party?
(Maria邀请了20个同学去她家里参加生日Party,如果3/5的同学是女孩,剩余是男孩,那么Maria邀请了多少女同学参加Party呢?)
你看这个题目文字就比较复杂,让孩子一步到位把图画出来不太可能,那怎么通过阅读进行分解呢?我们来操作一下!
首先孩子读这一段“Maria’s going to celebrate her birthday at home and invited 20 classmates.”,这句话其实想表达的意思是“Maria邀请了20个同学”。
那么我们就画出下面的图:

再看下面一句话“If we know that 3/5 of the class are girls and the rest are boys”,这句话的意思是“3/5的同学是女孩”。
那么我们就把图分成5份:

接着取其中的3份,那就代表了3/5的女同学:

这张图画出来后,孩子再列出相应的数学表达式就很简单了!
我们画了5个格子,那么每个格子代表:20 / 5 = 4,也就是说每个格子代表4个孩子。
而女同学占3个格子,那么她们一共有:3 x 4 = 12,也就是说女同学一共有12人。
你看通过一步一步解读题目,并在每一步画出相应的图,这道题就逐渐迎刃而解了!
刚才题目还比较简单,当遇到更复杂的题目,这个建模的价值就越发体现出来了。比如我们看下面这道题:
William has 130 model cars in total. He has 4 times as many convertibles than cars that aren’t convertibles. How many convertibles does William have?
(William有130个汽车模型,他的敞篷汽车数量是不敞篷的4倍,问他有几个敞篷汽车模型?)
对于这种题目,学过方程的人会习惯用方程去求解,但其实用建模的话,解这种题目会非常容易。
这道题目也是需要分步画图,首先画出非敞篷车模型(绿色部分),然后画出敞篷车模型(红色部分),注意后者是前者的4倍,最后总数是130。模型如下:
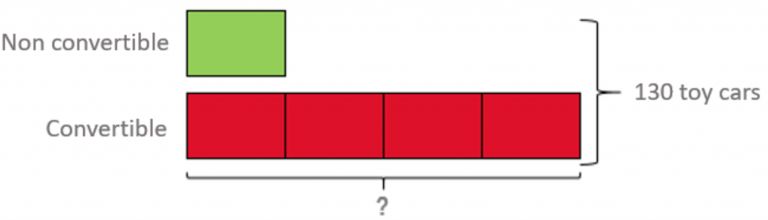
这样孩子就知道敞篷车的数量了,只要130除以5个格子,算出每个格子对应的车数量,后面就能得到答案!
Part.3 资源分享
关于建模,我以前分享给你们新加坡数学关于建模的教学网站,那个网站极好,基本上关于加减乘除、比较问题、总和问题等数学应用题的基础题型那里分析得都非常详细。
我之前教憨憨数学的时候,就把那个网站的内容好好参考了一番,受益匪浅,所以也推荐给你们!
你们在我公号对话框回复 建模,就能得到新加坡数学关于建模的教学网站了,不过网站是全英文的!
ps. 微信改版后对话框不好找,点击标题下方“憨爸在美国”,然后“进入公众号”,点击底部“文章目录”左边的键盘图标,会出现像微信聊天一样可以打字的地方,在那里输入关键词就会有回复给您了。
扫描二维码
在里面回复
建模

相关阅读
我们研究了几千份美国课堂思维导图教学案例,编写了一本《硅谷工程师爸爸的超强思维导图课》,专门针对数学、英语、阅读、写作、科学等学科,教孩子如何运用思维导图塑造学习型大脑。这本书也曾是当当新书销售榜冠军。点击左下角 阅读原文 可以购买!


憨爸在美国
硅谷工程师爸爸,分享美式教育理念和资源,专注于英语、数学、科学启蒙,一定让你脑洞大开哟!

公号ID:hanhanusa
微博:@憨爸在美国